Как бы выглядел граф если бы все пять карандашей обменялись подарками

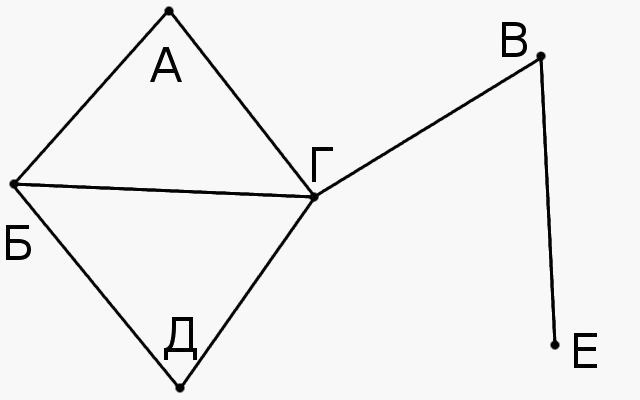
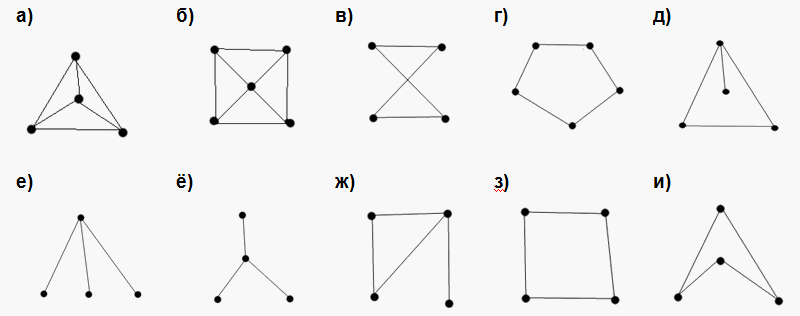
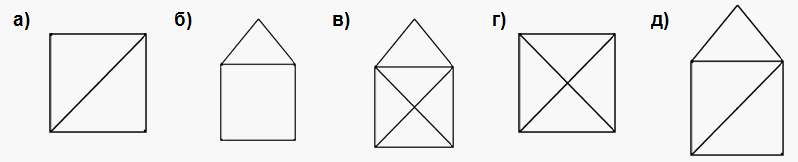
Посчитаем для каждого графа пару чисел: число его вершин и число его рёбер. Если у графов отличается число вершин или число рёбер, то они не могут быть одинаковыми.

Графы Б и Г отличаются от остальных числом вершин (у них по 5 вершин, а у остальных по 4) и друг от друга числом рёбер. Поэтому они ни с кем больше не одинаковые.

Из оставшихся графов только у графа А 6 ребёр, поэтому он тоже ни с кем не одинаковый.

У графов Е и Ё по 4 вершины и по 3 ребра. Легко проверить, что они одинаковые.

У оставшихся графов В, Д, Ж, З, И по 4 вершины и по 4 ребра. Но у них разные степени вершин: у графов В, З, И степени всех вершин равны 2, а у графов Д и Ж по две вершины степени 2 и по одной вершине степеней 1 и 3. Легко убедиться, что В=З=И и Д=Ж, но В≠Д. Таким образом, мы перечислили все наборы одинаковых графов и доказали, что других нет.

Кёнигсбергские мосты

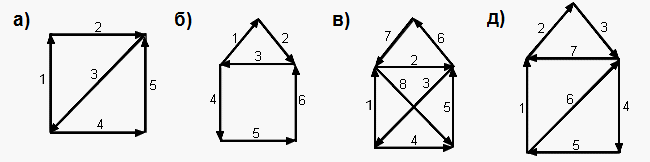
а, б, в, д) На рисунке ниже показано, как можно нарисовать каждый из этих графов одним росчерком. Последовательность и направление обхода показаны цифрами и стрелками:

г) В графе из пункта г есть четыре вершины нечётной степени 3, поэтому в силу задачи 5 его нельзя нарисовать одним росчерком.

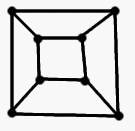
У куба 12 рёбер по 1 см, а у нас есть ровно 12 см проволоки. Значит, делать двойные рёбра нельзя, иначе нам не хватит проволоки.

Каркас куба можно изобразить в виде графа:

Разные задачи

Рассмотрим одного из этих шестерых. Назовём его А. Среди остальных пяти у него обязательно есть либо трое знакомых, либо трое незнакомых.

Сначала рассмотрим случай, когда А знаком по крайней мере с тремя другими: B, C и D. Если хоть какие-то двое из этих троих знакомы между собой (например, В и С), то мы получаем тройку попарно знакомых людей А, В, С. Если же они все незнакомы между собой, то мы получаем тройку попарно незнакомых: B, C и D.

Аналогично рассматривается случай, когда А не знаком по крайней мере с тремя другими (назовём их снова B, C и D). Если хоть какие-то двое из этих троих не знакомы между собой (например, В и С), то мы получаем тройку попарно незнакомых людей А, В, С. Если же они все знакомы между собой, то мы получаем тройку попарно знакомых: B, C и D.

Докажем, что город с картой, приведённой в ответе, удовлетворяет условию задачи.

Сначала докажем, что улицы этого города нельзя обойти, пройдя каждую по одному разу. Если бы это было возможно, то и граф, изображающий карту города, можно было бы нарисовать одним росчерком (просто рисуя соответствующий маршрут обхода улиц). А этого сделать нельзя в силу задачи 5: в этом графе все четыре вершины имеют нечётную степень 3.

Следующий рисунок показывает, как можно обойти улицы этого города, пройдя каждую по два раза. Для наглядности мы изображаем каждую улицу двумя рёбрами и показываем цифрами порядок обхода улиц. Красной точкой отмечено начало и конец маршрута.

Источник статьи: http://mmmf.msu.ru/archive/20122013/z6/18.html

Презентация на тему «Контрольная работа «Логические рассуждения», информатика, 3 класс

Разработка учителя информатики МОУ «СОШ №20» г. Новомосковска Тульской области Поспеловой Галины Васильевны Логические рассуждения

Цели урока: Проведение контрольной работы Закрепить полученные знания: о множестве, элементе множества, подмножестве, пересечении и объединении множеств; о высказывании , истинности высказывания, об отрицании; о графе, о графе с направленными рёбрами.

Закрась все белые карандаши на рисунках красным цветом. Впиши в таблицу слова «ДА» и «НЕТ». 1 На рисунке НЕТ серого карандаша НЕТ ДА НЕТ ДА 2 На рисунке больше трёх карандашей И есть серый карандаш НЕТ НЕТ ДА НЕТ 3 На рисунке есть карандаш (серый ИЛИ красный) ДА НЕТ ДА ДА Проверка домашнего задания 37

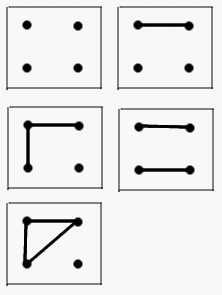
Прочитай описание. Соедини линиями точки графа. 39 Пять волшебных карандашей, которые познакомились на конкурсе рисунков, сделали друг другу подарки на память. Красный карандаш подарил свои рисунки жёлтому и синему, оранжевый – красному и жёлтому, зелёный — оранжевому, а синий – зелёному. Какие из карандашей сделали подарков больше, чем получили? Ж С О К З Ж С О К З Как выглядел бы граф, если бы все пять карандашей обменялись подарками? Сколько рисунков нужно для этого сделать каждому карандашу?

Прочитай описание и соедини стрелками точки графа. 40 Лучшими на конкурсе были три рисунка: «Автомобиль», «Бабочка» и «Парусник». Красный карандаш рисовал все три картины. Жёлтый карандаш помогал ему нарисовать автомобиль, а синий и зелёный – парусник. Бабочку рисовали все пять карандашей. Ж С О К З А Б П

Прочитай описание и раскрась каждую страну на рисунке. 41 Из всех городов Зелёной страны приехали гости во все оранжевые города. Из всех городов Розовой страны участники конкурса приехали в один из оранжевых городов. Гости Жёлтой страны приехали НЕ из всех своих городов, но они побывали во всех городах Оранжевой страны. Синяя страна тоже прислала на конкурс жителей НЕ всех своих городов, и они посетили НЕ все оранжевые города.

Домашнее задание № 42, 43 (стр.25)

Источники: Информатика в играх и задачах. 3 класс: Методические рекомендации для учителя. – авт.-сост. А. В.. Горячев, К. И. Горина. — М.: Баласс, 2009. – 128 с. Информатика в играх и задачах. 3-й класс. Учебник в 2-х частях, часть 2 – 56 с. М.:Баласс, 2010.

Источник статьи: http://xn--j1ahfl.xn--p1ai/presentation/18602.html

Разработка учителя информатики МОУ «СОШ 20» г. Новомосковска Тульской области Поспеловой Галины Васильевны. — презентация

Презентация была опубликована 6 лет назад пользователемМаргарита Мынкина

Презентация на тему: » Разработка учителя информатики МОУ «СОШ 20» г. Новомосковска Тульской области Поспеловой Галины Васильевны.» — Транскрипт:

1 Разработка учителя информатики МОУ «СОШ 20» г. Новомосковска Тульской области Поспеловой Галины Васильевны

3 Закрепить полученные знания: о множестве, элементе множества, подмножестве, пересечении и объединении множеств; о высказывании, истинности высказывания, об отрицании; о графе, о графе с направленными рёбрами.

4 Закрась все белые карандаши на рисунках красным цветом. Впиши в таблицу слова «ДА» и «НЕТ». 1На рисунке НЕТ серого карандаша НЕТДАНЕТДА 2На рисунке больше трёх карандашей И есть серый карандаш НЕТ ДАНЕТ 3На рисунке есть карандаш (серый ИЛИ красный) ДАНЕТДА 37

5 Прочитай описание. Соедини линиями точки графа. 39 Пять волшебных карандашей, которые познакомились на конкурсе рисунков, сделали друг другу подарки на память. Красный карандаш подарил свои рисунки жёлтому и синему, оранжевый – красному и жёлтому, зелёный — оранжевому, а синий – зелёному. Какие из карандашей сделали подарков больше, чем получили? Ж С О К З Ж С О К З Как выглядел бы граф, если бы все пять карандашей обменялись подарками? Сколько рисунков нужно для этого сделать каждому карандашу?

6 Прочитай описание и соедини стрелками точки графа. 40 Лучшими на конкурсе были три рисунка: «Автомобиль», «Бабочка» и «Парусник». Красный карандаш рисовал все три картины. Жёлтый карандаш помогал ему нарисовать автомобиль, а синий и зелёный – парусник. Бабочку рисовали все пять карандашей. Ж С О К З А Б П

7 Прочитай описание и раскрась каждую страну на рисунке. 41 Из всех городов Зелёной страны приехали гости во все оранжевые города. Из всех городов Розовой страны участники конкурса приехали в один из оранжевых городов. Гости Жёлтой страны приехали НЕ из всех своих городов, но они побывали во всех городах Оранжевой страны. Синяя страна тоже прислала на конкурс жителей НЕ всех своих городов, и они посетили НЕ все оранжевые города.

10 1. Информатика в играх и задачах. 3 класс: Методические рекомендации для учителя. – авт.-сост. А. В.. Горячев, К. И. Горина. — М.: Баласс, – 128 с. 2. Информатика в играх и задачах. 3-й класс. Учебник в 2-х частях, часть 2 – 56 с. М.:Баласс, 2010.

11 Учитель информатики МОУ «СОШ 20» г. Новомосковск Тульская область, 2011 г.

Источник статьи: http://www.myshared.ru/slide/857412/

Графы. Применение графов к решению задач

1. Методические рекомендации к теме “Графы”.

Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. Важно, чтобы ученики сразу осознали, что один и тот же граф может быть нарисован разными способами. Строгое определение графа, на мой взгляд, давать не нужно, т.к. оно слишком громоздко и это только затруднит обсуждение. На первых порах хватит и интуитивного понятия. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Важно, чтобы ученики до конца разобрались в ее доказательстве и научились применять к решению задач. При разборе нескольких задач рекомендую не ссылаться на теорему, а фактически повторять ее доказательство. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.

Первая и главная цель, которую нужно преследовать при изучении графов, –научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов. Не стоят рассказывать обе всем на нескольких занятиях подряд. Лучше разнести занятия по времени на 2–3 учебных года. (Прилагается разработка занятия “Понятие графа. Применение графов к решению задач” в 6 классе).

2. Теоретический материал к теме “Графы”.

Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.

Рассмотрим две задачи.

Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.

Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?

Решение: Занумеруем последовательно клетки доски:

А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:

Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.

Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.

Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:

Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.

Степени вершин и подсчет числа ребер графа

Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.

С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.

Задача 3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?

Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным . Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.

Ответ. Соединить телефоны таким образом невозможно.

Теорема: Любой граф содержит четное число нечетных вершин.

Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.

Есть еще одно важное понятие, относящееся к графам – понятие связности.

Граф называется связным, если из любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.

Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.

Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:

Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.

Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”

Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:

Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:

Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.

Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.

Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?

Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.

Сейчас мы доказали теорему об Эйлеровых графах:

Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.

И в заключение – задача о Кенигсбергских мостах.

Задача 7. На рисунке изображена схема мостов города Кенигсберга.

Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?

3. Задачи к теме “Графы”

Понятие графа.

1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?

Рис. 1

Решение. Занумеруем клетки доски, как показано на рисунке:

Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:

При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.

2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?

Решение. Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.

Степени вершин и подсчет числа ребер.

3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.

Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.

4. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?

Ответ. Нет (теорема о четности числа нечетных вершин).

5. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?

Ответ. Нет, не может.

6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?

Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.

7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.

Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.

Связность.

8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.

Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.

Графы Эйлера.

9. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист

а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?

10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?

Источник статьи: http://urok.1sept.ru/articles/416943

Как бы выглядел граф если бы все пять карандашей обменялись подарками